마르코프 결정 과정(MDP)
- MDP란? RL에서 환경(environmnet)을 설정하는 것이다. t+1의 상태는, 오직 이전인 t상태만 고려!
1. Markov Processor

- 마르코프 프로세스란, 특정 상태에서 다른 상태로 전이할 확률P를 의미한다.
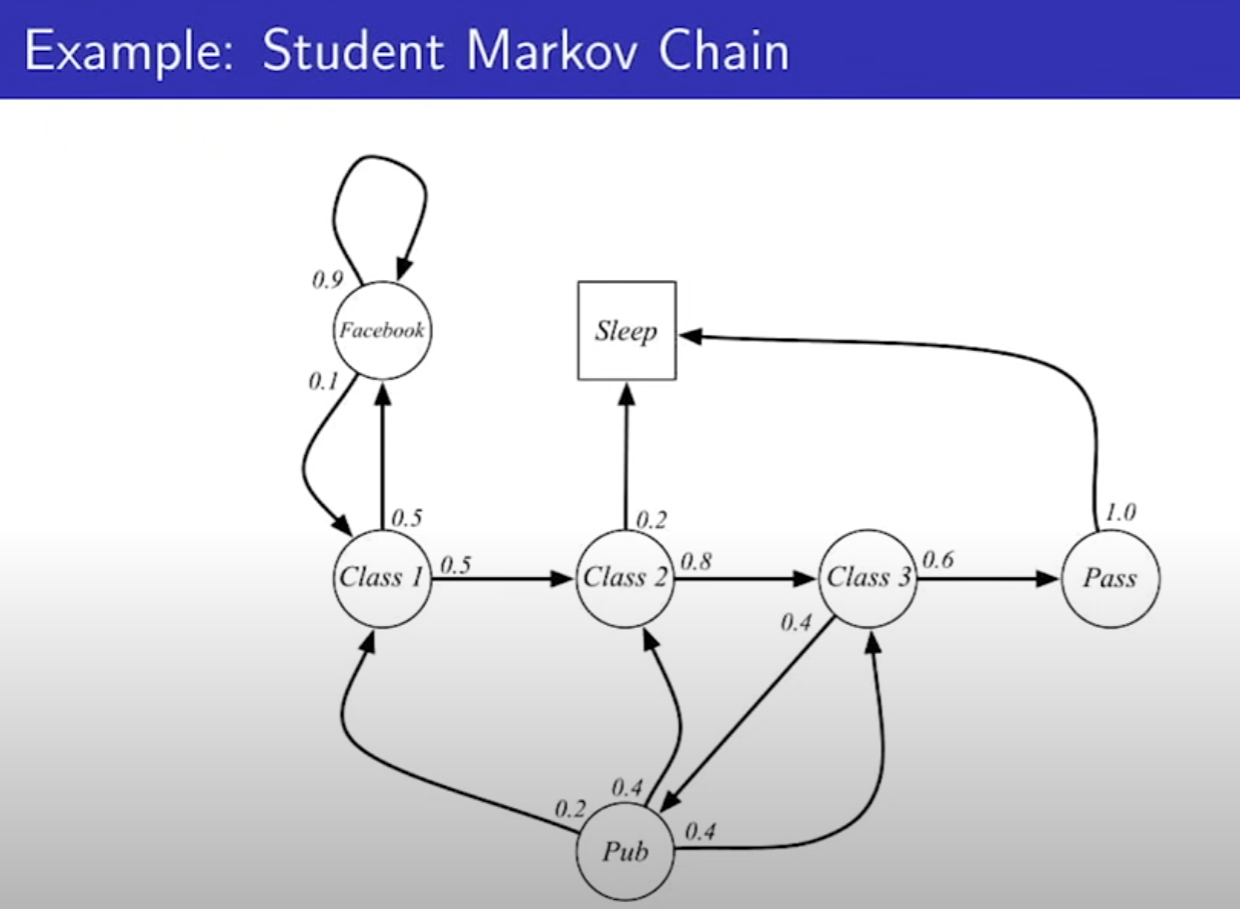
- State는 7개, 화살표는 State의 전이하는 것. 확률도 써있다. Sleep는 마지막 종료 프로세스로 생각하면 된다. Pass로 가면 무조건 Sleep으로 가서 끝낸다.
- 에피소드(episode)는 랜덤한 한 상태에서 시작하여, 특정 상태에 도달하는 것 까지의 과정을 에피소드라고 한다. 에피소드를 여러개 하는것을 샘플링이라고 한다. 에피소드 하나를 샘플이라고 볼 수 있다.

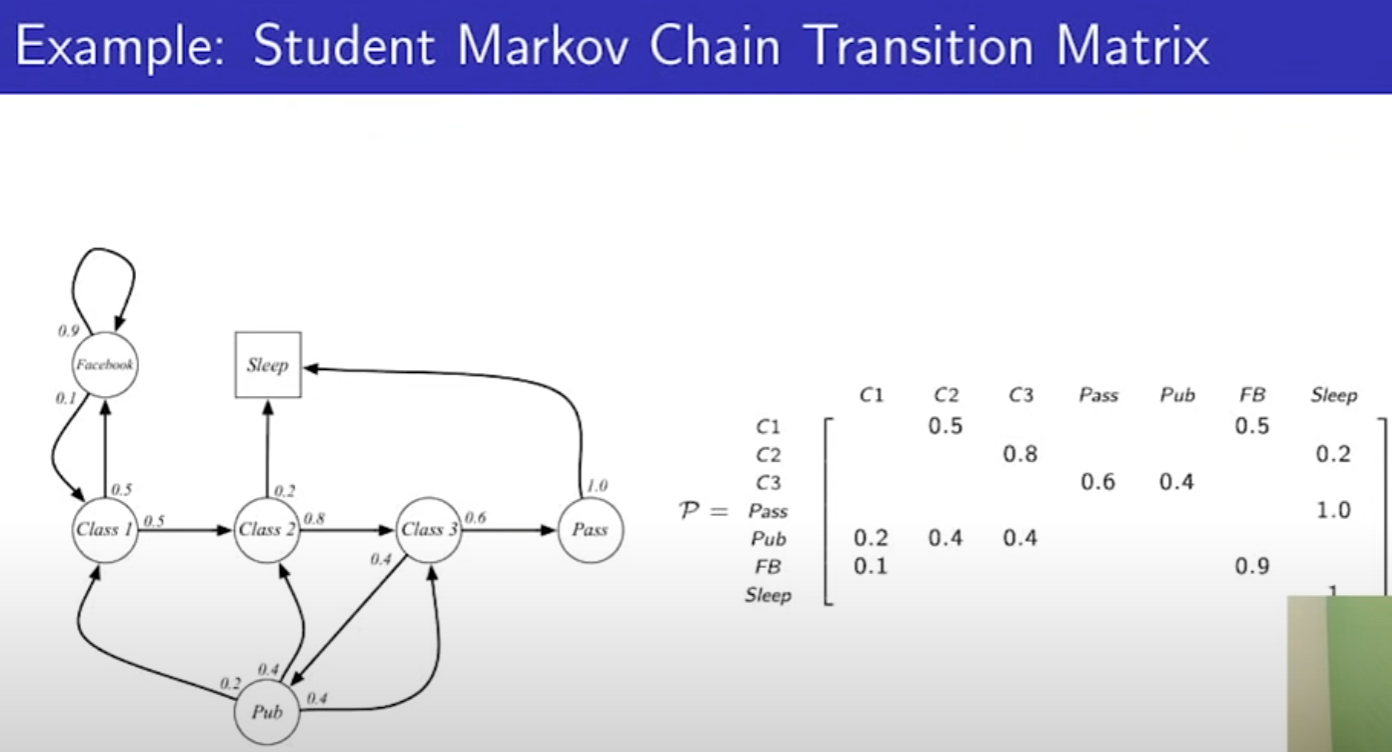
-State Transition Matrix: t상태에서, t+1의 상태로 전이할 확률, 즉 현재 상태에서 다음 상태를 결정하는 확률이다. 예를들어P1n은 1번방에서 시작하여 2번방 3번방 ... n번방을 가게될 확률이다.
2. Markov Reward Processes(MRP)

S(State), P(상태 전이 확률), R(Reward, 어떤 상태에 도착 시 보상 정의), r(감마, discount factor)

- 리워드는 action에 따라서가 아닌, 도착한 State에 따라 리워드를 정해주고 있다.

- 우리는 Return을 최대화 하는게 목표, 즉 Reward와 r(감마, 0~1사이의 값)의 총합이 최대가 되게 하는게 목표다.

discount를 하는 이유는 다양하다. 수학적으로 편리하다.

- Value Function은 return의 기댓값이다. 샘플링을 하며 에피소드가 하나씩 생기는데, 각 샘플(에피소드)의 리턴값의 합이다. E는 기댓값을 뜻한다.

- 각 에피소드의 v를 다 더해서 평균낸 것이 State-Value Function이다. 예시에서는 S1(C1)을 구할 수 있다.
- MRP, MDP의 Value Function은 다르다. MDP에서는 정책(Policy)에 따라 행동했을 때의 기대값이다.
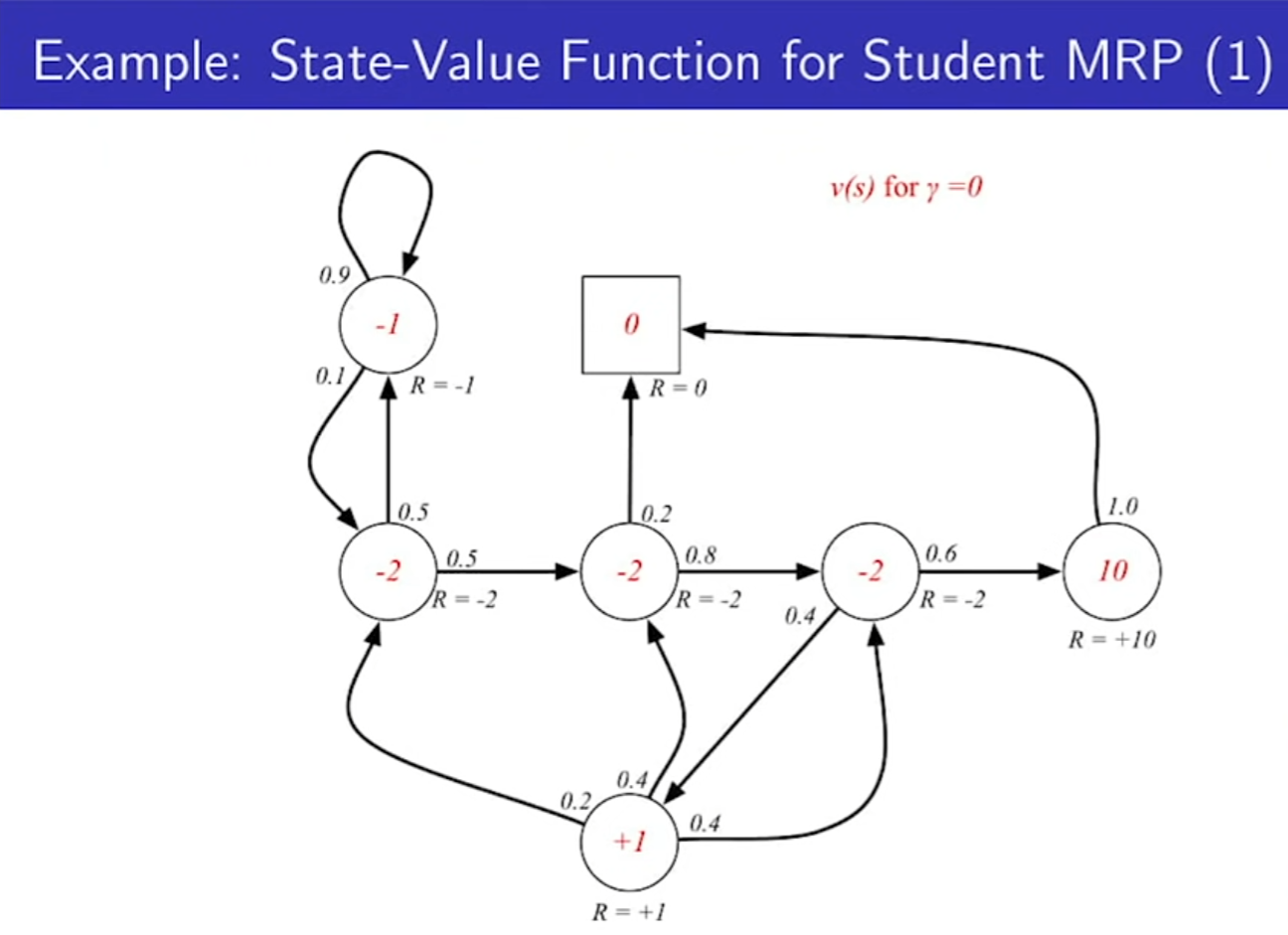
- 구하는 방법은 추후에 설명한다.

- 벨만의 방정식은, Gt(리턴값)를 풀어서, 가치 함수를 리워드 + r(감마)기댓값 으로 표현된다.

- 결국 v(s) = Rs + r(상태 s에서 특정 상태로 갈 확률 X v(s')) 가 된다.
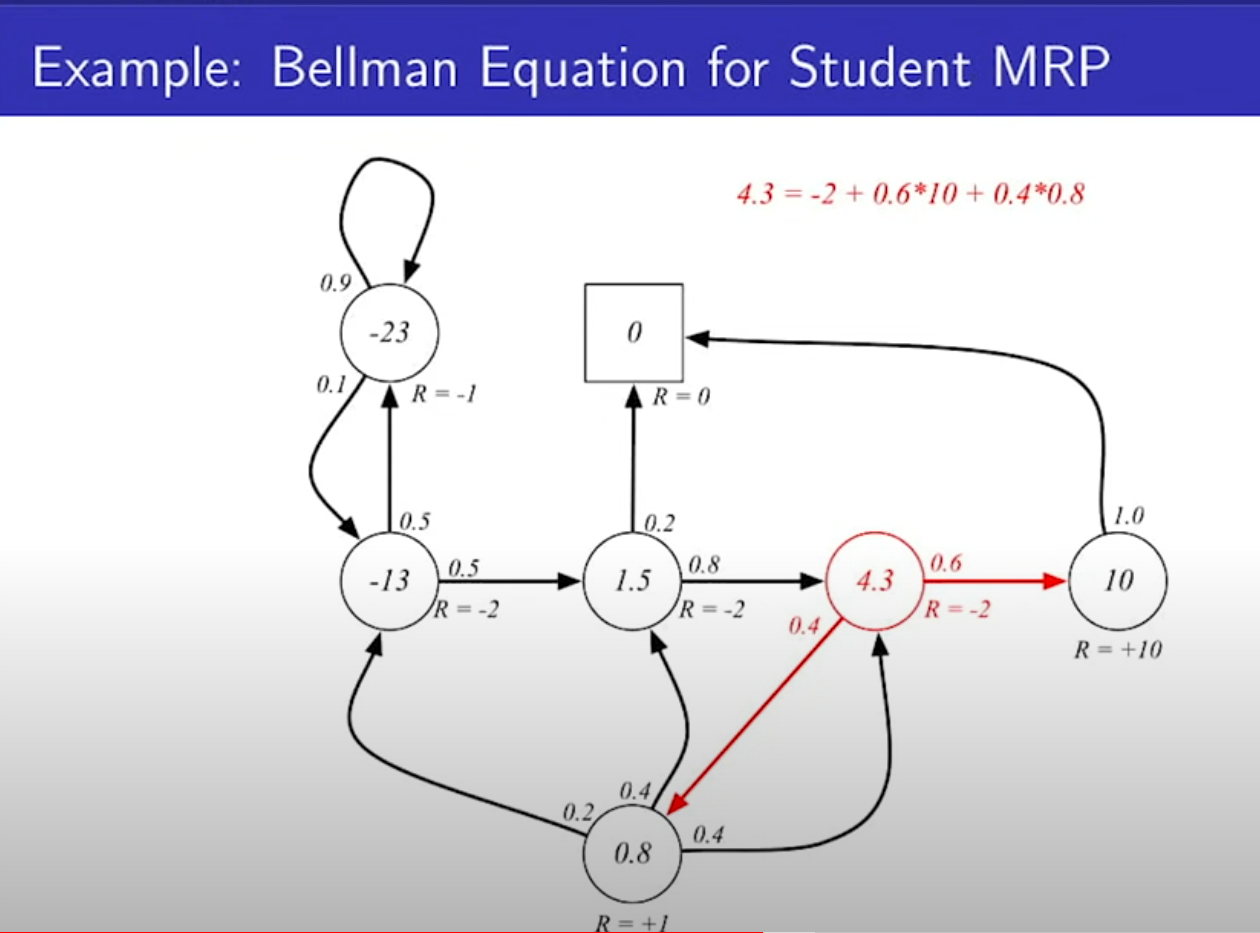
- 각 상태의 값을 구하는건 뒤에서 한다. 검증 해보면 답이 맞다. 각 상태의 value는 이전 상태가 정해져야 정할 수 있으므로 되게 복잡하다.

-

- R, P, r가 주어져 있으면 우리는 v를 구할 수 있다. 컴퓨터는 GPU로 행렬식을 계산하면 빠르기 때문에 행렬 자주 사용. 시간 복잡도가 n의 3제곱이라, 작은 규모에서만 사용하길 권장한다.
3. Markov Decision Processes

- MRP에서 Action이 추가됨.
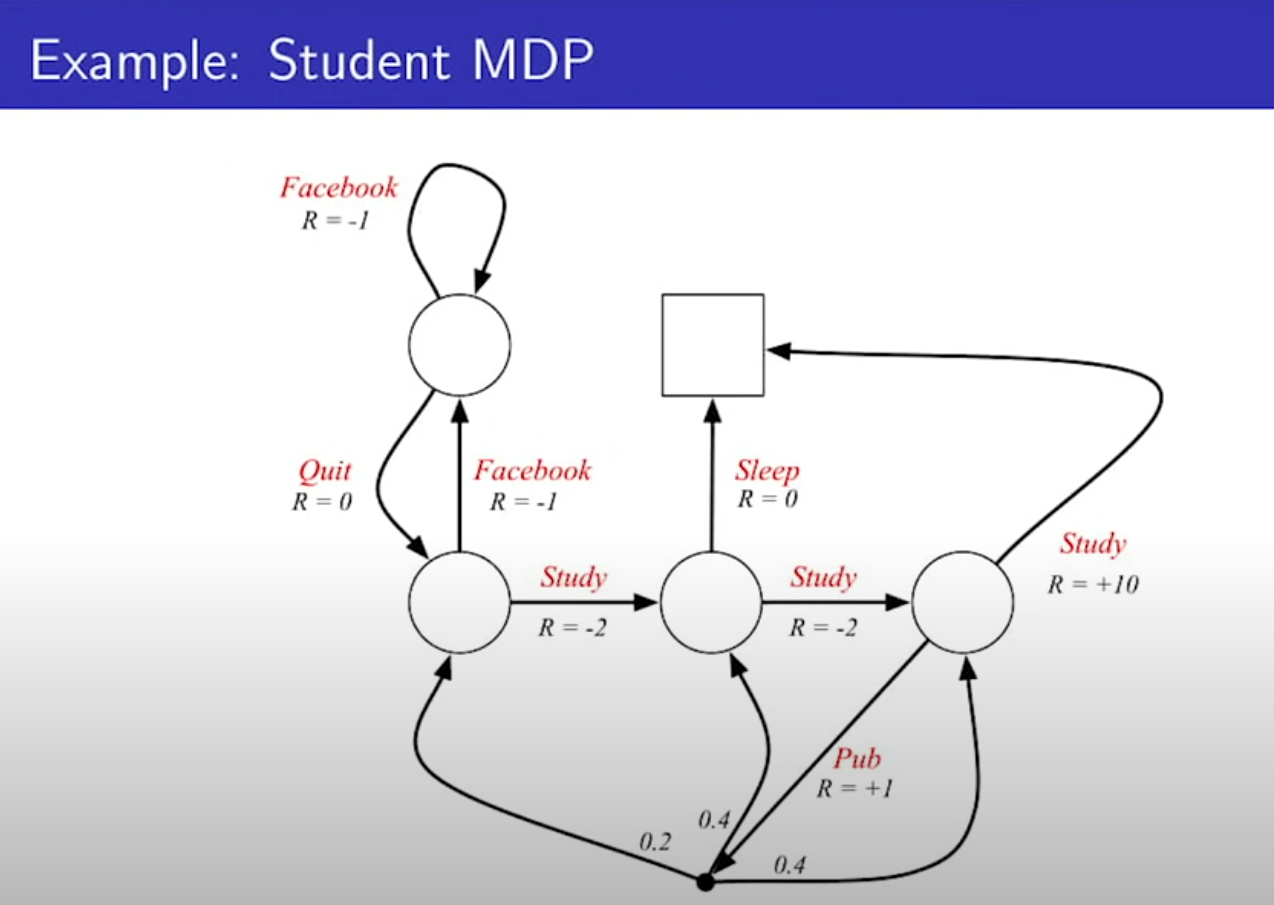
- Action으로 Study, Sleep, Facebook 등이 추가됨. 여기서 추가적으로 Action을 한다고 무조건 화살표 방향대로만 가는게 아닌, 해당 액션을 취할 확률도 있고, 액션을 취했을때 원하는 곳(State)으로 갈 확률이 따로 있다. 보통 100%로 가정한다. Pub쪽을 보면 Pub 행동을 하면 3갈래로 나뉜다. Pub을 취할 확률 + Pub 액션을 취했을때 State로 갈 확률이 또 있는 것이다.

- Action마다 State가 달라지기 때문에, 정책이 필요하다. s상태에서, Agent가 a를 취할 확률이다. 현재 상태만 알면 구할 수 있다.

- MDP에서 에이전트가 어떤 정해진(고정된) 정책을 따라 특정 액션을 취해서, State에서 S'으로 갈 확률은 마르코프 프로세스와 동일하다. 정책이 고정되어 있기 때문이다.
- State와 Reward는 MRP와 동일하다.

- Value Function은 역시 정책을 추가해서, 샘플링을 통해 v(기댓값(Return))들의 평균을 구한 것이다.
- Action Value Function(q)은 상태 s에서 특정 행동 a를 했을 때, 그 이후에는 정책 파이에 따라 게임을 끝까지 했을때의 기대값이다.

- 여기서 모든 s에서 특정 행동을 할 정책 파이는 0.5, discount는 1이다. 계산법은 추후에 배운다.

- 벨만의 기대 방정식, 현재 상태 s에서의 state-value function은, 일단 한 스텝을 가고 그거에 대한 보상 Rt+1에, 그 다음 state에서부터 정책 파이를 따라 가는 것과 동일하다. action value function도 동일.

- state에서 action을 할 확률과 그 액션을 했을때의 q(Action Value Function)를 곱한 가중치의 합이 v다.

- 반대로 q를 v로 표현할 수도 있다. q는, 현재 상태 s에서 행동 a를 한 Reward + S에서 모든 스테이트 s'로 갈 확률 곱하기 상태 s'의 value를 곱한 것의 합에 discount를 해준게 q다.

- 위 식을 대입해보면, 행렬로 만들기에 좋은 형태가 된다.
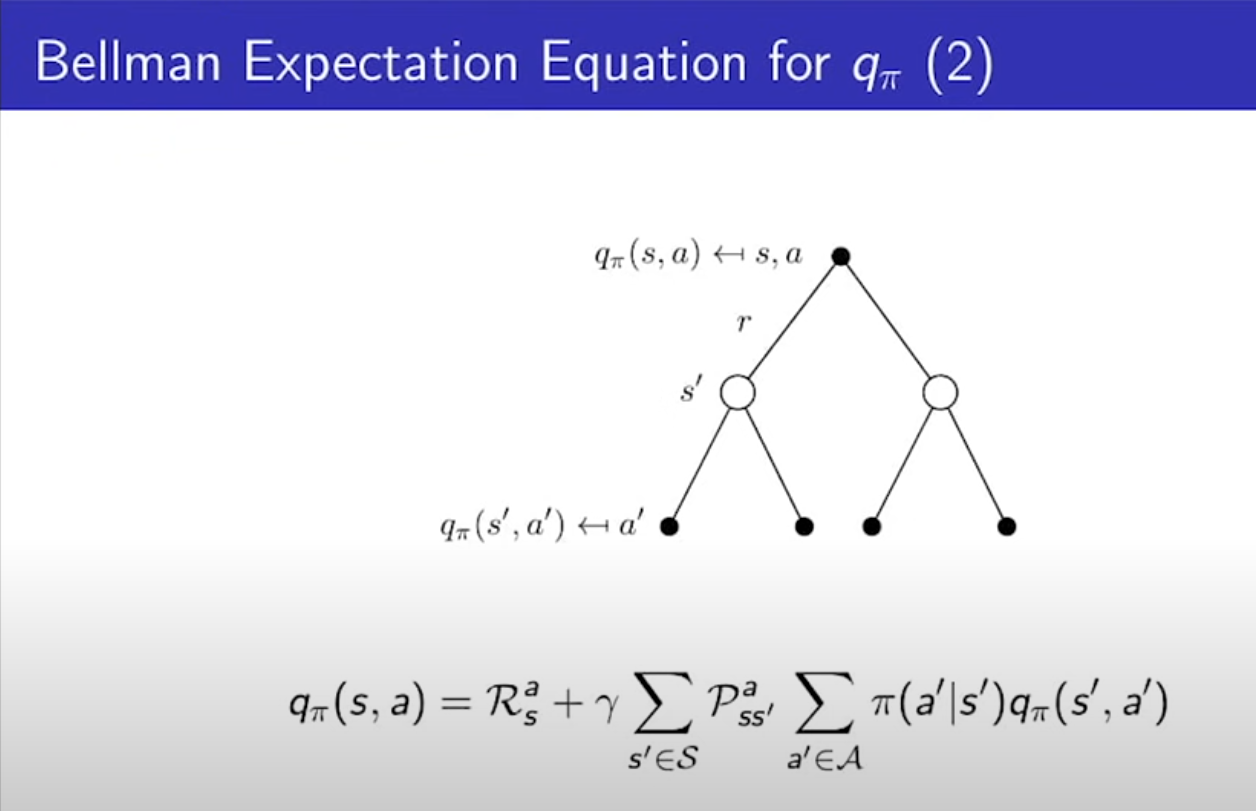
- 이런게 있다고 넘어가자.
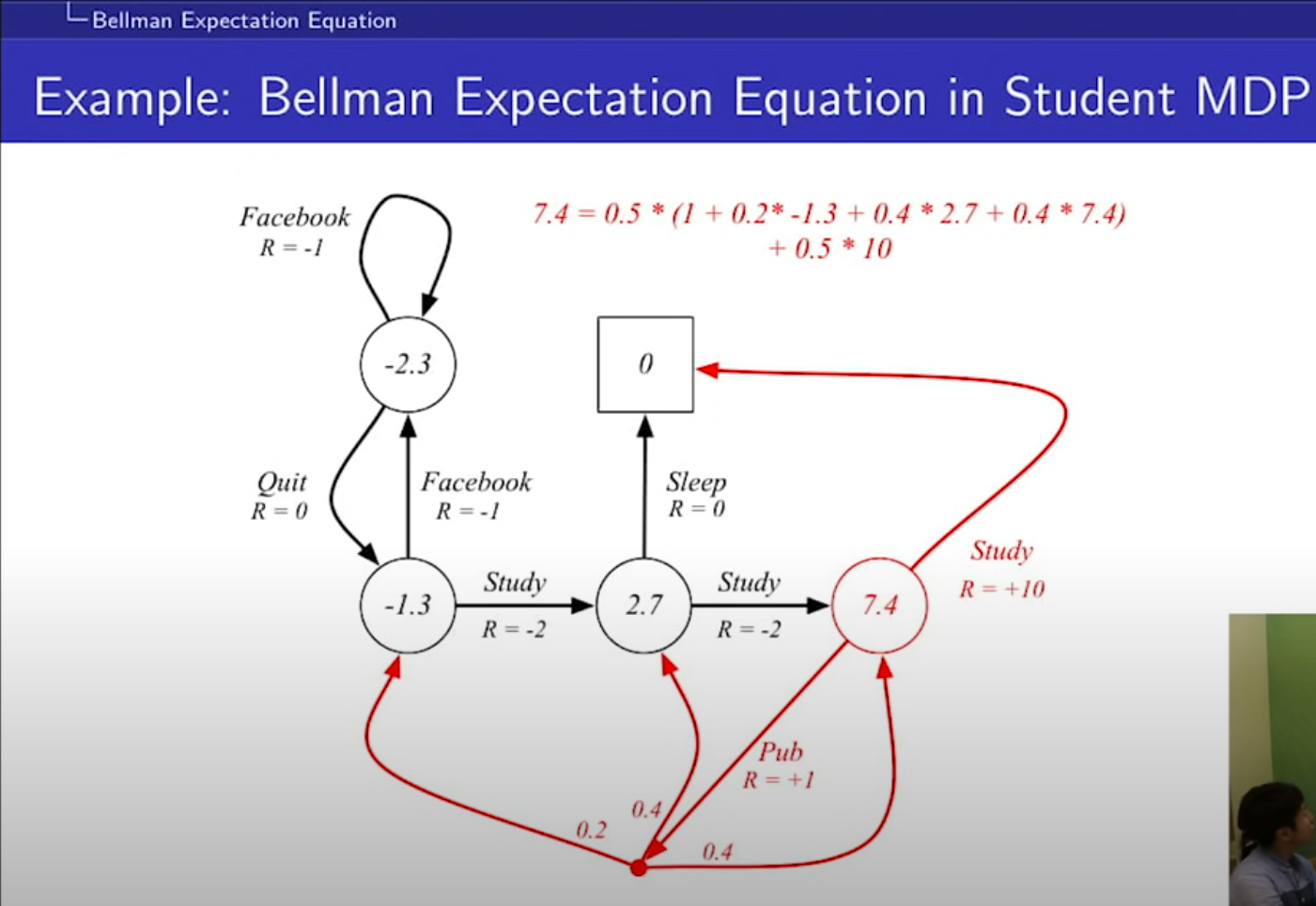
- 똑같이 계산해보면 7.4를 구할 수 있다.

- 벨만의 기대 방정식을 이용해, MRP로 표현해 볼 수 있다.
벨만의 기대 방정식은 정책 P가 확률로 기대되어서 풀기 쉬웠지만, 이제는 어려워진다.

- optimal state-value function은 v스타(s)로 표현한다. 이는 정책이 무한개 있고, 정책에 따른 value function도 무한개 있을탠데, 여러 정책중에서 가장 최적의 value 찾는 것이다.
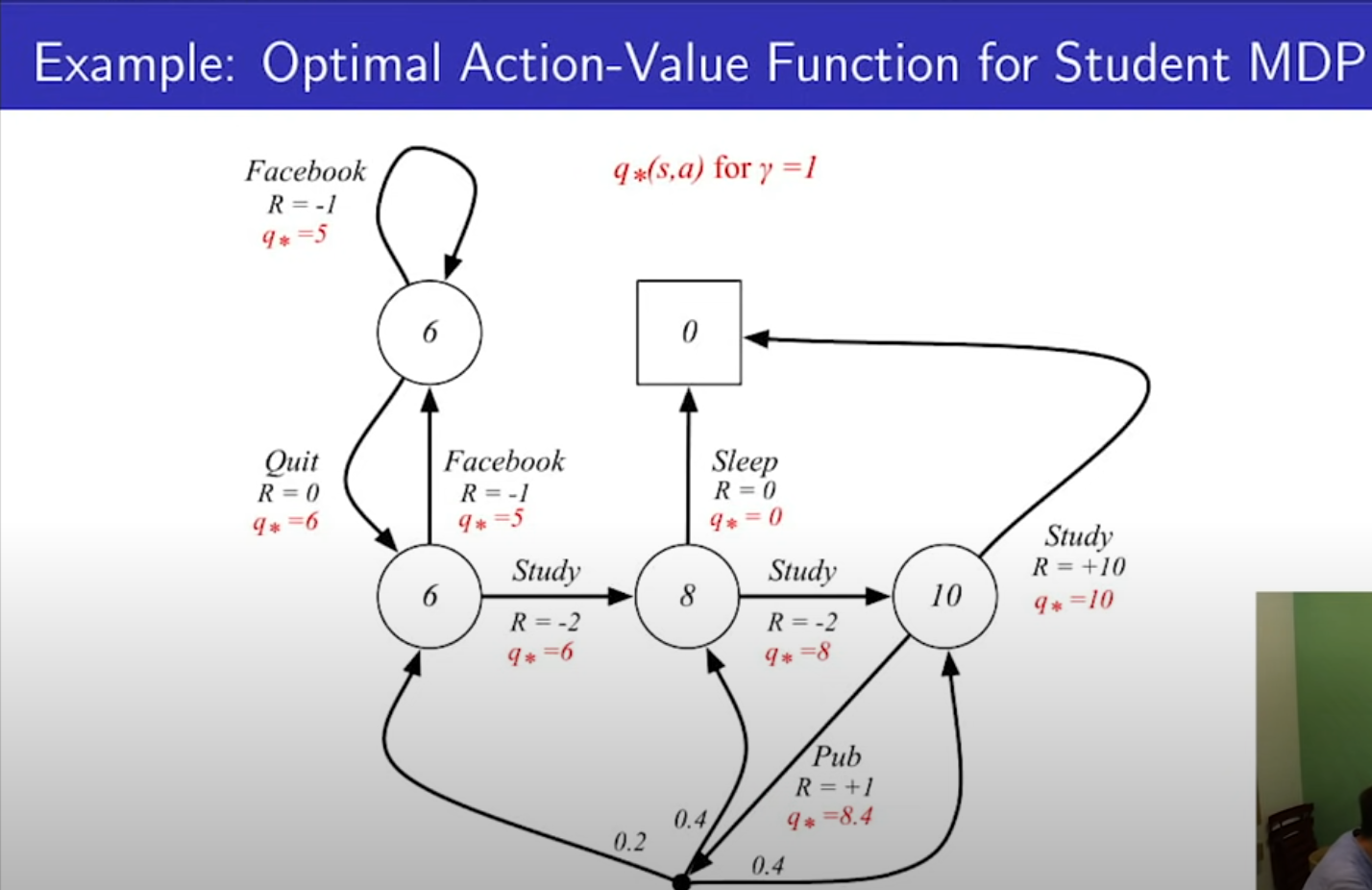
- 감마가 1일때 optimal value function과 q를 나타낸다.

- Optimal Policy를 정리하기 위해서는, 먼저 여러 정책중 어느 정책이 나은지를 찾아야 한다. 정책 파이가 파이프라임보다 좋다. 모든 State s에 대해서, v파이(s)가 v파이'(s)보다 클때만 인정된다.
- 모든 MDP에 대해서, optimal policy가 존재하는데, 파이(스타)는 모든 파이(정책)에 대하여 partial ordering이 성립한다. 모든 상태에서 가장 좋다고 증명이 되어있다.
- 모든 optimal policies는 모두 가장 큰 value function을 가진다. q도 동일, 여기서 정책은 모두 같은 optimal policies가 아닐 수 있음. 여러개의 policies 일 수 있다.

- optimal policies는 q(스타)를 알면 무조건 하나는 찾아진다.
- MDP에서는 항상 결정적인 정책이 있다. 무조건 그 정책에 따라 특정 행동만 한다는 것이다. 그것이 optimal policy이기 때문이다. ex) 가위바위보에서 상대가 가위바위보를 3/1 확률로 낸다고 치면, 에이전트는 무조건 바위만 내면 그게 가장 최적의 정책이다.
- 우리는 q(스타)를 구하면 optimal policy를 구할 수 있다. 즉, 문제를 해결한 것이다.
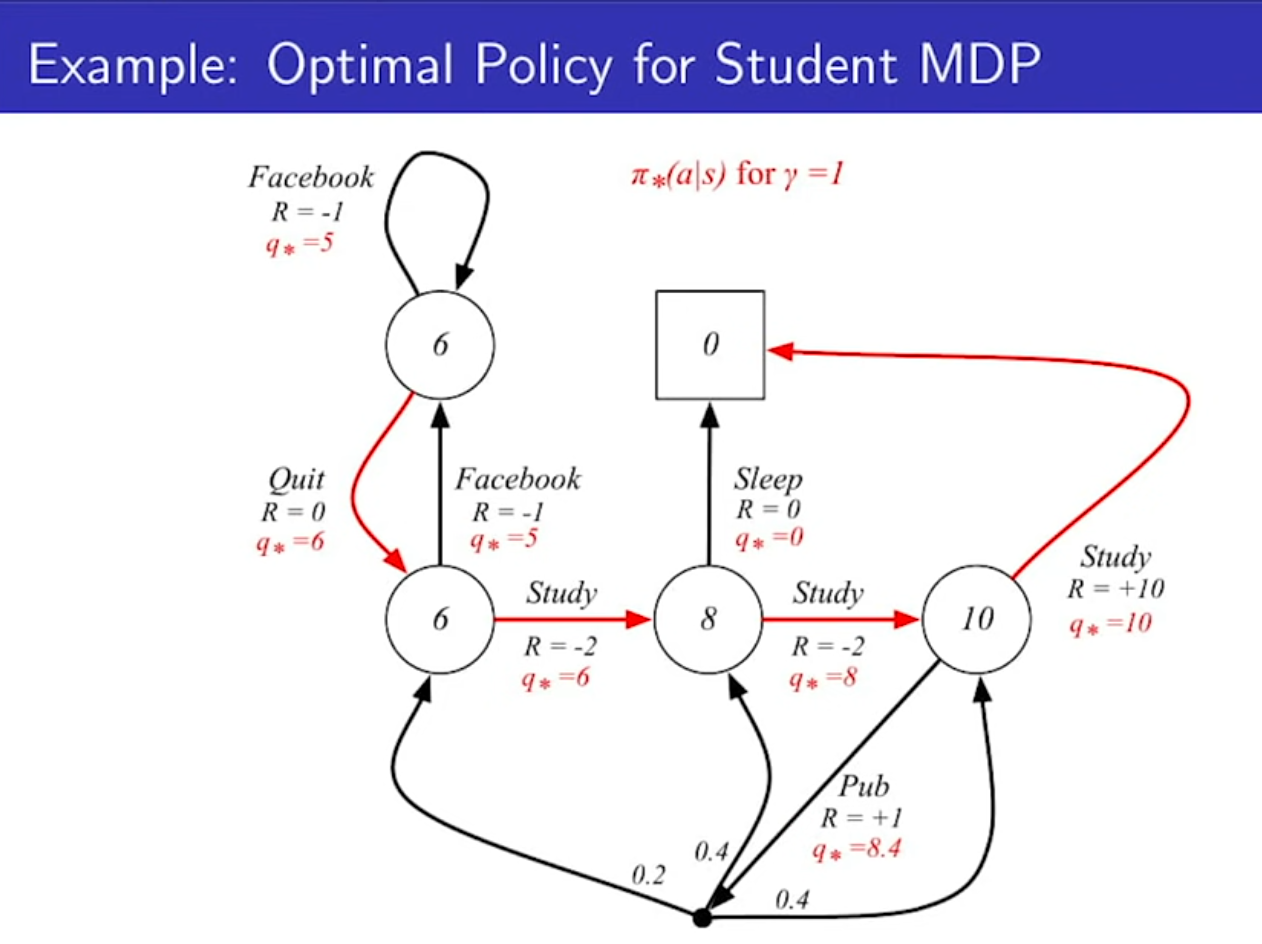

- max만 붙는다.


- max값은 선형 방정식이 아니기 때문에, 행렬로 풀 수가 없다.

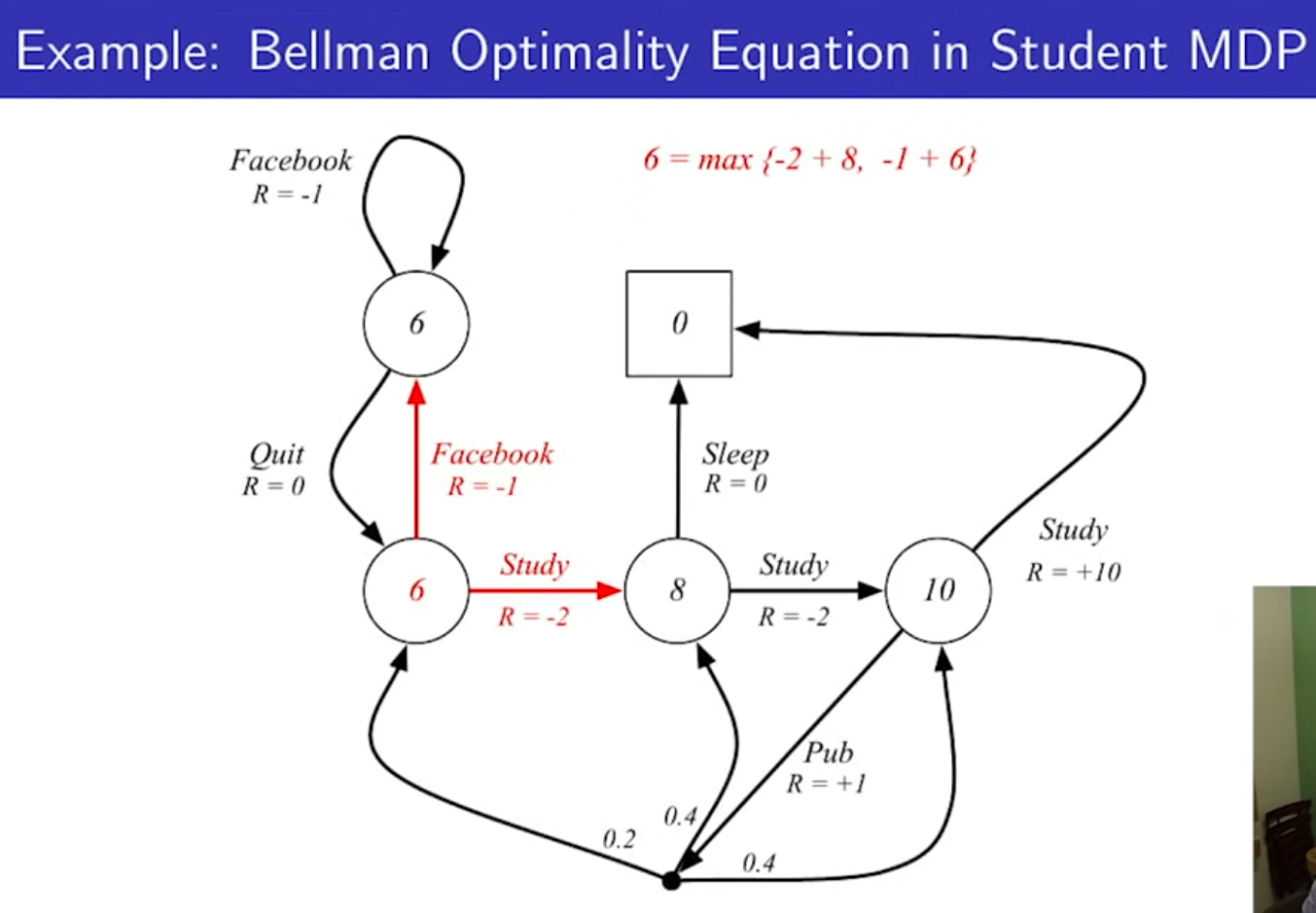

- 벨만의 최적 방정식은 선형 방정식이 아니라, 솔루션(해)가 일반적으로 없다
- 다른 반복적인 해법들이 있다.
'AI > 강화학습' 카테고리의 다른 글
| 1. [OpenAI] Spinning Up in Deep RL Introduction (1) | 2025.01.16 |
|---|---|
| Model Free Control (0) | 2024.06.25 |
| Model Free Prediction (0) | 2024.06.16 |
| Planning by Dynamic Programming (0) | 2024.06.15 |
| 강화학습 소개(David Silver) (0) | 2024.05.11 |



