Control - 환경을 모를 때 최적의 정책을 찾는 것

- 저번 강의에선 MDP를 모를 때 value를 찾는 prediction 문제에 대해 다룸
- 이번 강의에선 MDP를 모를 때 최적의 정책을 찾는 것을 다룸(최적의 가치 = 최적의 정책)

- On-policy는 내가 최적화하고자 하는 정책과 환경에서 경험을 쌓는 정책이 같은 것
- Off-policy는 다른 에이전트가 행동한 경험들을 통해 배우는 정책 방법
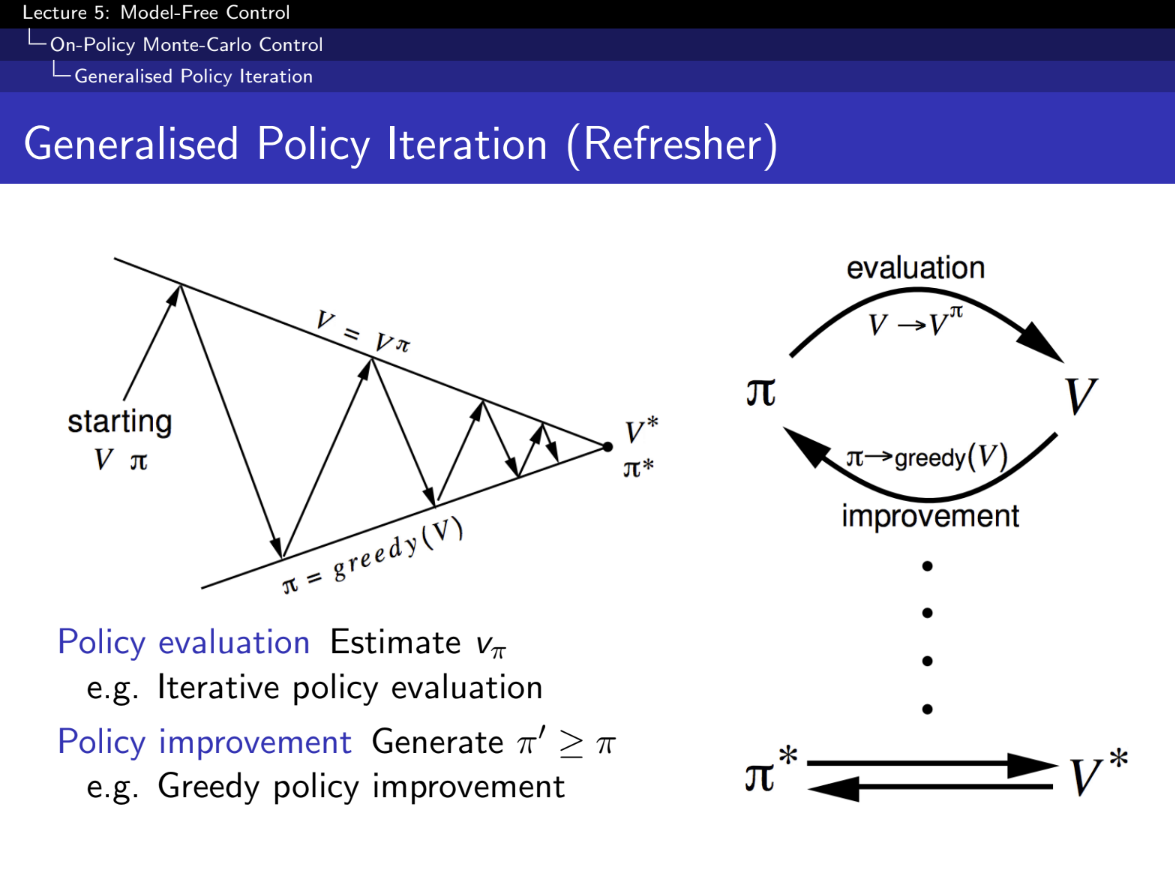
- 정책 평가 (Policy Evaluation):
- 현재 정책 π\pi에 대해 상태가치 함수 VπV^\pi를 추정합니다.
- 예: 반복 정책 평가 (Iterative Policy Evaluation)
- 정책 개선 (Policy Improvement):
- 현재 정책 π\pi를 사용하여 새로운 정책 π′\pi'를 생성합니다. 여기서 π′≥π\pi' \geq \pi입니다.
- 예: 탐욕적 정책 개선 (Greedy Policy Improvement)

- 몬테 카를로도 evaluation으로 가능한가?
- 정책 평가:
- 몬테카를로 정책 평가를 사용하여 V=vπ 추정
- 정책 개선:
- 탐욕적 정책 개선 방법을 사용하여 새로운 정책을 생성합니다.
위 방법으로 하면 최적의 정책을 찾는 것 아닌가? - 안된다.
- 내 다음 State를 알아야 Greedy(다음 상태중에 가장 VALUE가 높은 쪽으로 가는 것)하게 가능한데, 현재 MDP를 모르는 상태다. 불가능!
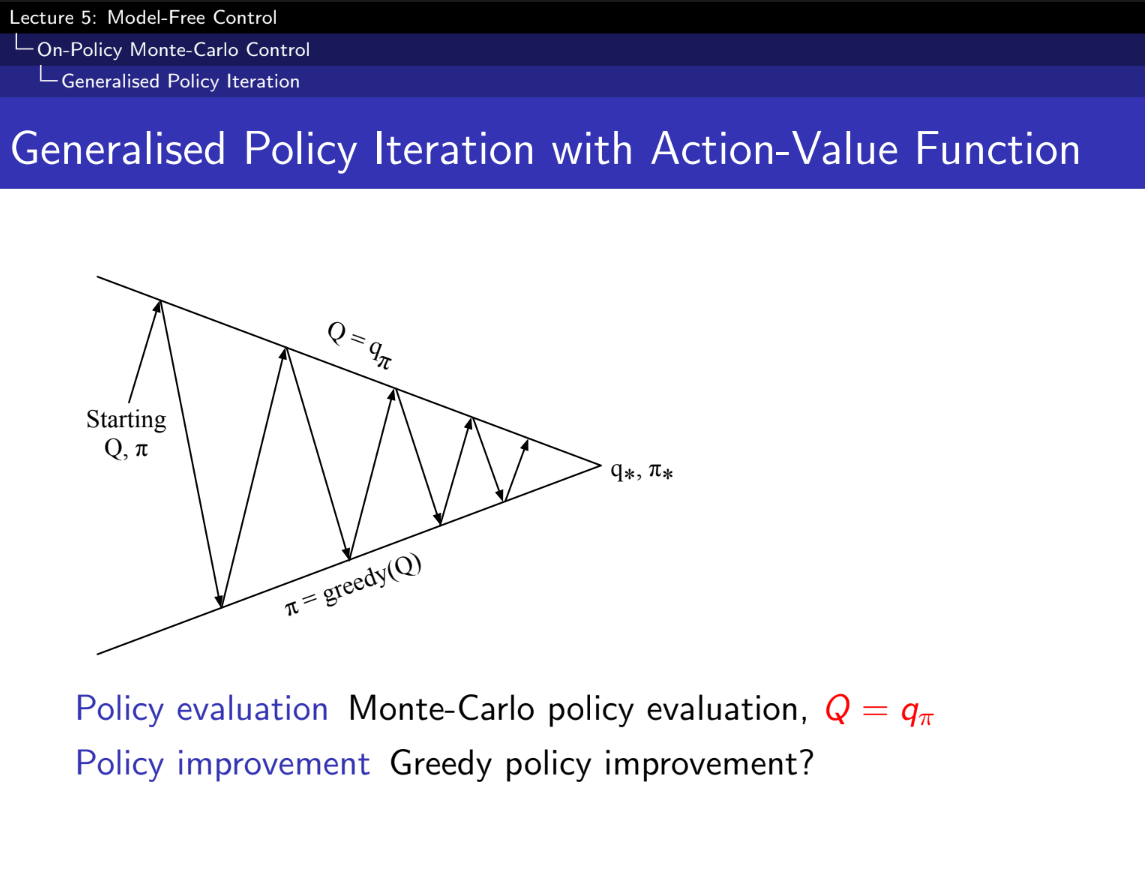
- MC를 이용해 Q를 찾아내고, Greedy policy improvement를 사용하면 되겠네? No!
- Greedy하게 움직이면 충분히 많은 곳으로 갈 수 없다. 아래 사진을 보면 문제점 예시이다.

- 처음 연 왼쪽문 +점수만 가지고는, 오른쪽이 무조건 좋다고 할 수 없는데, greedy하게 가면 무조건 오른쪽만 연다.
- 그래서 나온게 입실론-Greedy

- Exploration(탐험)을 보장, 여러곳을 갈 수 있다.
- 입실론의 확률로 랜덤하게 무작위로 행동한다. 예를들어 입실론이 0.05면, 0.95확률로 가장 좋은 곳을 찾아가고, 0.05 확률로 랜덤하게 간다.

- 입실론-greedy 사용하면 가능하다.
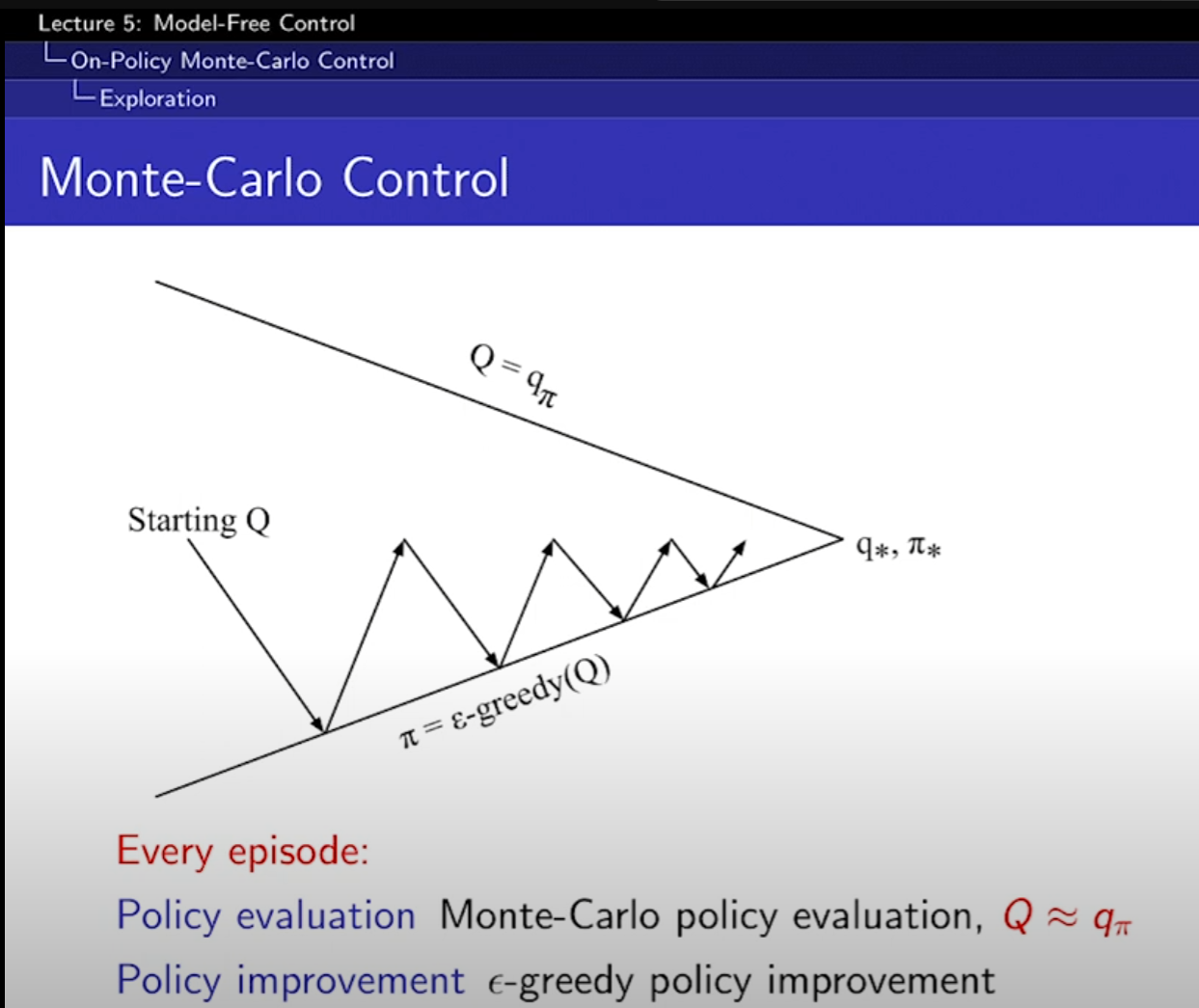
- 한 에피소드만 MC방법 쓰고, 바로 입실론-greedy 사용.
- 더 빨리 greedy 해서 유용하다. 잘 수렴하기 위해선 몇가지 성질이 필요하다. (GLIE)

- 모든 State, Action 들이 무한히 반복되어야 exploration을 충분히 할 수 있다.
- 결국에는 policy가 입실론-greedy policy가 greedy policy로 수렴해야 한다. (0.05확률로 바보같은 행동을 하는데 최적이냐?에 대한 물음)

- 위 조건들을 만족하면 GLID Monte-Carlo Control이다.


- MC말고, TD Control도 가능하다. S에서 A행동을 해서 R보상을 받고 S'상태에서 다시 A'액션을 하는 것. Sarsa 라고 함

- TD기 때문에 한 에피소드가 아닌, 한 스텝마다 Q가 업데이트가 된다! 극단적이다. Sarsa 알고리즘이다.

- Q 테이블(state와 action에 관한)을 만든다.
- A 행동중에 하나를 뽑는다. 액션에 대한 리워드와 다음 state(S')를 관측, S'에서 랜덤한 행동 A'를 또 골라서 Q를 업데이트 한다.
- 위 사항 반복하면 Sarsa 알고리즘이다.

- 다음 두 조건이 만족하면 Sarsa 알고리즘은 optimal action-value function이다.
- GLIE(모든 State, Action에 접근해야되고, 입실론이 줄어들어서 결국 greedy policy에 수렴해야한다)
- 알파가 1~무한까지 더하면 무한이 되어야 한다. 스텝사이즈가 충분히 커야한다. 알파제곱의 합이 무한보다 작다. q밸류를 수정하는게 결국 수렴한다는 것. 실제 사용할때는 이 두 조건은 별로 신경쓰지 않아도 policy를 잘 찾는다.

- Sarsa도 TD처럼 가능하다. n-Step, 람다, Backward 등
1. TD 학습 (TD Learning)
- 기본 아이디어: TD 학습은 현재 상태에서 다음 상태로 이동할 때의 차이를 사용하여 가치 함수나 정책을 업데이트합니다. TD(0)라고도 합니다.
- 업데이트 공식: Q(st,at)←Q(st,at)+α(rt+1+γQ(st+1,at+1)−Q(st,at))Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right)
- 장점: 샘플 효율적이며, 미래의 예측을 반영하여 업데이트합니다.
- 단점: 단일 스텝만을 고려하므로 학습이 느릴 수 있습니다.
2. N-step SARSA
- 기본 아이디어: N-step SARSA는 단일 스텝 대신 N개의 스텝을 사용하여 더 긴 기간 동안의 보상을 고려하여 업데이트합니다.
- 업데이트 공식: Q(st,at)←Q(st,at)+α(∑k=0N−1γkrt+k+1+γNQ(st+N,at+N)−Q(st,at))Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( \sum_{k=0}^{N-1} \gamma^k r_{t+k+1} + \gamma^N Q(s_{t+N}, a_{t+N}) - Q(s_t, a_t) \right)
- 장점: 더 많은 정보를 사용하므로, 업데이트가 더 정확할 수 있습니다.
- 단점: 적절한 N값을 선택하는 것이 어렵고, 계산량이 증가할 수 있습니다.
3. λ(람다) Forward SARSA (SARSA(λ))
- 기본 아이디어: SARSA(λ)는 TD(0)와 Monte Carlo 방법 사이의 균형을 맞추기 위해 시간차의 가중 평균을 사용합니다. λ는 가중치 감소율을 나타냅니다.
- 업데이트 공식: Q(st,at)←Q(st,at)+α(Gt(λ)−Q(st,at))Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( G_t^{(\lambda)} - Q(s_t, a_t) \right) 여기서 Gt(λ)G_t^{(\lambda)}는 λ-반복 수렴 (λ-return)입니다.
- 장점: 다른 시간 차원에서의 정보를 결합하여 더 안정적인 학습을 가능하게 합니다.
- 단점: λ값을 적절히 선택하는 것이 중요하며, 계산 복잡도가 증가할 수 있습니다.
4. Backward SARSA
- 기본 아이디어: Backward SARSA는 자가 예측을 통한 추정 방법으로, 후방에서의 TD 에러를 사용하여 업데이트합니다. 흔히 엘리젤릭 트레이스를 사용합니다.
- 업데이트 공식: e(st,at)=λγe(st−1,at−1)+1e(s_t, a_t) = \lambda \gamma e(s_{t-1}, a_{t-1}) + 1 Q(st,at)←Q(st,at)+αδte(st,at)Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \delta_t e(s_t, a_t) 여기서 e(st,at)e(s_t, a_t)는 엘리젤릭 트레이스이며, δt\delta_t는 TD 에러입니다.
- 장점: 효율적인 메모리 사용과 빠른 수렴 속도를 가질 수 있습니다.
- 단점: 복잡한 추적 관리와 적절한 λ값 설정이 필요합니다.
비교 요약
- TD 학습: 단일 스텝 기반의 간단한 업데이트, 느린 학습 속도.
- N-step SARSA: 여러 스텝을 반영하여 보다 정확한 업데이트, 계산 복잡도 증가.
- SARSA(λ): 다양한 시간 차원 정보를 가중 평균, 안정적이나 λ 설정이 중요.
- Backward SARSA: 후방 추적과 TD 에러 사용, 메모리 효율적이나 복잡도 증가.
이 방법들은 각기 다른 상황과 요구에 맞춰 사용될 수 있으며, 보상 신호와 학습 환경에 따라 적절한 방법을 선택하는 것이 중요합니다.
더 설명하자면,
λ(람다) Forward SARSA
λ(람다) Forward SARSA는 현재 시점에서 앞으로 여러 스텝 동안의 반환값(Return)을 고려하여 가중치를 줍니다. 이는 여러 스텝의 보상과 추정값을 조합하여 가치 함수를 업데이트합니다.
- 기본 개념:
- λ(람다)는 미래의 보상에 대한 가중치 감소율을 나타냅니다.
- 현재 시점에서 여러 스텝에 걸쳐 얻은 보상들을 가중 평균하여 사용합니다.
- 업데이트 방식:
- 각 스텝마다 미래의 여러 스텝에서 얻을 보상들을 가중치 λ를 적용하여 결합한 값을 사용하여 가치 함수를 업데이트합니다.
- Gt(λ)G_t^{(\lambda)}는 λ-반복 반환값(λ-return)으로, 이는 현재부터 앞으로의 여러 스텝에 걸친 보상들의 가중 합입니다.
- 업데이트 공식: Q(st,at)←Q(st,at)+α(Gt(λ)−Q(st,at))Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( G_t^{(\lambda)} - Q(s_t, a_t) \right)
- 여기서 Gt(λ)G_t^{(\lambda)}는 다음과 같이 정의됩니다: Gt(λ)=(1−λ)∑n=1∞λn−1Gt(n)G_t^{(\lambda)} = (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)} Gt(n)=∑k=0n−1γkrt+k+1+γnQ(st+n,at+n)G_t^{(n)} = \sum_{k=0}^{n-1} \gamma^k r_{t+k+1} + \gamma^n Q(s_{t+n}, a_{t+n})
- 이는 각 스텝마다 미래의 여러 스텝에서 얻을 보상들을 고려하여 가중치를 적용한 값을 업데이트에 반영하는 방식입니다.
Backward SARSA (with Eligibility Traces)
Backward SARSA는 과거의 경험을 반영하는 방식으로, 후방에서부터 가중치를 적용하여 업데이트합니다. 이 방법은 엘리젤릭 트레이스(eligibility trace)를 사용하여 과거의 상태-행동 쌍에 대한 가중치를 점진적으로 감소시키며 반영합니다.
- 기본 개념:
- 엘리젤릭 트레이스는 특정 상태-행동 쌍에 대한 책임의 정도를 나타내는 값입니다.
- 현재 시점의 TD 에러를 과거의 상태-행동 쌍에 누적하여 반영합니다.
- 업데이트 방식:
- 각 시점에서의 TD 에러 δt\delta_t를 계산하고, 이를 엘리젤릭 트레이스를 사용하여 과거의 상태-행동 쌍에 반영합니다.
- 엘리젤릭 트레이스는 다음과 같이 업데이트됩니다: e(st,at)=γλe(st−1,at−1)+1e(s_t, a_t) = \gamma \lambda e(s_{t-1}, a_{t-1}) + 1
- Q 값 업데이트 공식은 다음과 같습니다: Q(s,a)←Q(s,a)+αδte(s,a)Q(s, a) \leftarrow Q(s, a) + \alpha \delta_t e(s, a)
- 이는 현재의 TD 에러를 과거의 여러 상태-행동 쌍에 반영하여 업데이트하는 방식입니다.
요약
- λ(람다) Forward SARSA: 현재 시점에서 미래의 여러 스텝 동안의 반환값에 가중치를 주어 가치 함수를 업데이트합니다.
- Backward SARSA: 과거의 경험을 반영하여 현재의 TD 에러를 후방에서부터 가중치를 적용하여 가치 함수를 업데이트합니다.

- 다른 에이전트나 사람을 보고 배움
- 기존에 했었던 것이 있으면 사용하기 좋다.
- 탐험적인 행동을 하면서 안전하게 optimal policy를 배울 수 있다.
- 여러 정책들을 학습 가능
Off-Policy Learning - Important Sampling, Q-Learning

- 식을 알아야 한다. f(X)의 기댓값을 P를 이용해 구하고 싶다. P 주사위를 굴려서 Q의 기댓값을 구하고 싶은 경우, 정규 확률 P(X)와, 약간 확률이 다른 Q(X)로 구할 수 있다.
예시 설명
예를 들어, 우리가 어떤 주식의 일일 수익률을 분석한다고 가정해봅시다. 두 가지 분포가 있습니다:
- P(X)P(X): 주식 시장의 실제 분포
- Q(X)Q(X): 우리가 샘플을 얻을 수 있는 분포 (예: 모의 거래 데이터)
우리는 실제 주식 시장 분포 PP에서의 기대 수익률 EX∼P[f(X)]\mathbb{E}_{X \sim P}[f(X)]을 알고 싶지만, 실제 데이터가 부족합니다. 대신 모의 거래 데이터 QQ에서 샘플을 얻어 이를 추정할 수 있습니다.
단계별 설명
- 실제 기대값 정의:
- EX∼P[f(X)]=∑P(X)f(X)\mathbb{E}_{X \sim P}[f(X)] = \sum P(X) f(X)
- 이는 실제 분포 PP에서 함수 f(X)f(X)의 기대값입니다.
- 다른 분포 QQ로 변환:
- P(X)f(X)P(X) f(X)를 Q(X)Q(X)를 이용해 다시 작성: ∑P(X)f(X)=∑Q(X)P(X)Q(X)f(X)\sum P(X) f(X) = \sum Q(X) \frac{P(X)}{Q(X)} f(X)
- 여기서 P(X)Q(X)\frac{P(X)}{Q(X)}는 중요도 가중치입니다. 이는 분포 QQ에서 샘플링된 데이터를 분포 PP에서 샘플링된 데이터로 조정하는 역할을 합니다.
- 기대값의 형태로 재작성:
- EX∼P[f(X)]=EX∼Q[P(X)Q(X)f(X)]\mathbb{E}_{X \sim P}[f(X)] = \mathbb{E}_{X \sim Q} \left[ \frac{P(X)}{Q(X)} f(X) \right]
- 이는 분포 QQ에서 샘플링한 데이터로부터 분포 PP에서의 기대값을 추정할 수 있음을 의미합니다.
실제 예시 적용
- 우리가 실제로 모의 거래 데이터 QQ에서 100개의 샘플을 얻었다고 가정해봅시다.
- 각 샘플 XiX_i에 대해 f(Xi)f(X_i)는 해당 샘플에서의 일일 수익률입니다.
- 우리는 P(Xi)Q(Xi)\frac{P(X_i)}{Q(X_i)}를 계산하여 각 샘플의 중요도 가중치를 구합니다.
- 각 샘플에 대해 중요도 가중치를 곱한 수익률을 평균 내어 실제 기대 수익률을 추정합니다.
이를 통해 우리는 실제 데이터를 직접 얻지 않더라도, 모의 거래 데이터에서 실제 분포의 기대값을 추정할 수 있습니다. 중요한 점은 각 샘플의 중요도 가중치를 정확히 계산하여 분포의 차이를 보정하는 것입니다.

- 몬테카를로 Off-Policy, 각 샘플들의 값들을 곱하면, 직접적인 에피소드들은 아니지만, 결국 value를 찾을 수 있다는 것. 현실적으로 불가능하다. 왜냐하면 해당 변수가 너무 커서 동작을 할 수가 없다. 그래서 TD를 쓴다.

- TD를 사용하거나, Q-Learning으로 변수값을 크게 줄일 수 있다.

- 오프-정책 학습 (Off-Policy Learning):
- 정의: 학습 중에 취하는 행동(행동 정책 μ\mu)과 최적의 행동을 취하기 위한 정책(목표 정책 π\pi)이 다를 때, 이를 오프-정책 학습이라고 합니다.
- Q-러닝은 대표적인 오프-정책 학습 방법입니다.
- 중요도 샘플링이 필요하지 않음:
- Q-러닝은 중요도 샘플링을 사용하지 않습니다. 즉, 행동 정책 μ\mu와 목표 정책 π\pi의 비율을 계산하여 조정할 필요가 없습니다.
- 이는 Q-러닝이 목표 정책 π\pi의 가치 추정을 직접 업데이트하기 때문입니다.
- 행동 정책 (μ\mu)를 사용하여 다음 행동 선택:
- 학습 중에 에이전트는 행동 정책 μ\mu에 따라 행동 At+1A_{t+1}를 선택합니다. 이 행동 정책은 에이전트가 환경에서 실제로 수행하는 행동을 정의합니다.
- 대안 후속 행동 (A′A') 고려:
- 하지만 Q-러닝은 목표 정책 π\pi에 따라 대안 행동 A′A'를 고려하여 업데이트를 수행합니다.
- 즉, 다음 상태 St+1S_{t+1}에서 목표 정책 π\pi가 선택할 행동 A′A'를 사용합니다.
- Q-값 업데이트:
- 현재 상태-행동 쌍 (St,At)(S_t, A_t)에 대한 Q-값은 다음과 같이 업데이트됩니다: Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,A′)−Q(St,At))Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left( R_{t+1} + \gamma Q(S_{t+1}, A') - Q(S_t, A_t) \right)
- 여기서:
- Q(St,At)Q(S_t, A_t): 현재 상태-행동 쌍의 Q-값.
- α\alpha: 학습률.
- Rt+1R_{t+1}: 현재 상태 StS_t에서 행동 AtA_t를 수행한 후 받는 보상.
- γ\gamma: 할인율.
- Q(St+1,A′)Q(S_{t+1}, A'): 다음 상태 St+1S_{t+1}에서 목표 정책 π\pi가 선택할 행동 A′A'에 대한 Q-값.
요약
Q-러닝은 오프-정책 학습 방법으로, 중요도 샘플링을 사용하지 않고 행동 정책 μ\mu를 통해 다음 행동을 선택하지만, 목표 정책 π\pi를 통해 대안 행동을 고려하여 Q-값을 업데이트합니다. 이를 통해 목표 정책 π\pi를 따르는 최적의 Q-값을 학습합니다. 실제 행동 정책이 아닌, 목표 정책을 사용해 구할 수 있다.
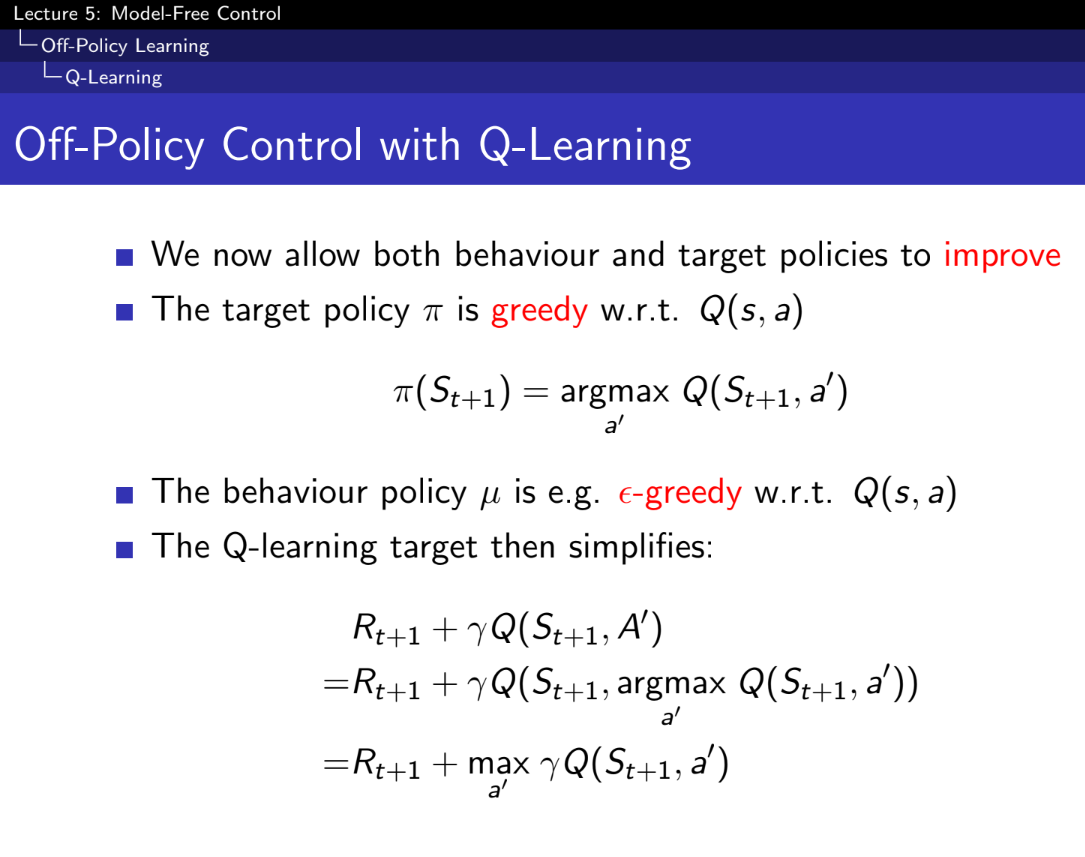
- 행동 정책도 improve 되면 좋겠다.
- 목표 정책은 greedy, 행동 정책은 입실론-greedy로 구한다.
- 이를 Q-러닝이라 한다

1. 벨만 기대 방정식(Bellman Expectation Equation)
- Full Backup (DP): Iterative Policy Evaluation
- 반복 정책 평가(Iterative Policy Evaluation)에서는 모든 상태에 대해 기대 값을 계산하여 정책의 가치 함수를 반복적으로 평가합니다.
- 그림에서 각 상태는 모든 가능한 다음 상태로의 전이를 고려하여 업데이트됩니다.
- Sample Backup (TD): TD Learning
- TD 학습에서는 현재 상태에서 샘플 하나를 사용하여 기대 값을 업데이트합니다.
- 그림에서 현재 상태와 다음 상태 간의 샘플 전이만을 사용하여 업데이트됩니다.
2. 벨만 기대 방정식(Bellman Expectation Equation)
- Full Backup (DP): Q-Policy Iteration
- Q-정책 반복(Q-Policy Iteration)은 상태-행동 가치 함수 qπ(s,a)q_\pi(s, a)를 반복적으로 평가하고 개선합니다.
- 모든 상태와 행동 쌍에 대해 모든 가능한 다음 상태와 행동을 고려하여 업데이트됩니다.
- Sample Backup (TD): SARSA
- SARSA는 현재 상태와 행동, 다음 상태와 행동을 사용하여 가치 함수를 업데이트합니다.
- 그림에서 현재 상태-행동 쌍과 다음 상태-행동 쌍을 사용하여 업데이트됩니다.
3. 벨만 최적 방정식(Bellman Optimality Equation)
- Full Backup (DP): Q-Value Iteration
- Q-가치 반복(Q-Value Iteration)은 상태-행동 가치 함수 q∗(s,a)q_*(s, a)의 최적 값을 반복적으로 찾습니다.
- 모든 상태와 행동 쌍에 대해 가능한 모든 다음 상태와 행동을 고려하여 최적 값을 업데이트합니다.
- Sample Backup (TD): Q-Learning
- Q-러닝은 현재 상태와 행동, 다음 상태에서의 최적 행동을 사용하여 가치 함수를 업데이트합니다.
- 그림에서 현재 상태-행동 쌍과 다음 상태에서의 최적 행동을 사용하여 업데이트됩니다.
요약
방정식Full Backup (DP)Sample Backup (TD)
| 벨만 기대 방정식 vπ(s)v_\pi(s) | Iterative Policy Evaluation | TD Learning |
| 벨만 기대 방정식 qπ(s,a)q_\pi(s, a) | Q-Policy Iteration | SARSA |
| 벨만 최적성 방정식 q∗(s,a)q_*(s, a) | Q-Value Iteration | Q-Learning |
- Iterative Policy Evaluation: 모든 상태에 대해 반복적으로 가치 함수를 평가.
- Q-Policy Iteration: 상태-행동 가치 함수를 반복적으로 평가하고 개선.
- Q-Value Iteration: 최적의 상태-행동 가치 함수를 반복적으로 찾음.
- TD Learning: 샘플 하나를 사용하여 기대 값을 업데이트.
- SARSA: 샘플 상태-행동 쌍을 사용하여 가치 함수를 업데이트.
- Q-Learning: 샘플 상태-행동 쌍과 다음 상태에서의 최적 행동을 사용하여 가치 함수를 업데이트.
- 정리 -
- 1, 2장은 MDP를 알때,
- 3, 4, 5장은 MDP를 모를때
- 3장 - 동적 프로그래밍(DP, Model-Based), 4,5장 Model free들 에서 On- Policy,Off-Policy 배움
'AI > 강화학습' 카테고리의 다른 글
| Model Free Prediction (0) | 2024.06.16 |
|---|---|
| Planning by Dynamic Programming (0) | 2024.06.15 |
| Markov Decsion Processes(MDP) (0) | 2024.05.12 |
| 강화학습 소개(David Silver) (0) | 2024.05.11 |



