- Model Free : MDP에 대한 정보를 모르는 상황
- Prediction : 주어진 policy 에 대하여 value function 을 찾는 것
- 본 단원에서는 MDP에 대해 알 수 없는 상황에서 주어진 Policy를 평가하는 것, 즉 대응하는 value function을 찾는 것에 대해 배울 수 있습니다.

- DP는 MDP를 푼 것
- 이번 강의에선 Model-free prediction(value function 찾기)
- 다음 강의에선 정책 찾기

- 몬테카를로 - 직접 구하기 어려운 문제를, 직접 하나씩 해보면서 실제 값들을 통해서 추출하는 것


- 특정 상태에 처음 방문한 것만 카운팅함

- 특정 상태에 방문한 모든 방문 횟수를 카운트

- 몬테카를로는 결국 여러번 해본것의 평균을 구하는 것이다.
- Incremental Mean을 쓰면 우리는 각 에피소드의 결과값을 저장해둘 필요가 없이, 바로바로 적용이 가능하다.

- TD는, MDP에 대한 지식이 필요 없고, 실행해보는 거다. MC랑 다른점은 에피소드가 끝나지 않아도 배울 수 있다.
guess로 guess를 업데이트한다.

- 몬테카를로는 Gt의 값에 따라 업데이트 되는데, TD는 사진과 같은 식을 타겟으로 한다. t+1은 t시점 다음의 예측한 값들이다.

- MC와 TD의 비교!
- MC는 결과로 업데이트 하지만, TD는 한번 실행하고 예측값으로 다음 값을 업데이트 해준다.

- TD는 결과가 나오기 전에 학습이 가능하다. MC는 결과가 나와야 학습이 가능
- TD는 결과 없이 학습이 가능하다. MC는 결과가 완전해야만 학습 가능

- TD는 Bias하고, Variance(분산) 되어 있다. value function이 편향될 가능성이 높고, 랜덤한 에피소드를 여러번 돌렸을 때, 한 스텝마다 업데이트 하기 때문에 분산되어 있는 정도가 적다.

- 편향되어 있어 수렴하는 v도 편향되는 것 아니냐? 다행히 정상적으로 수렴한다고 증명되어 있다.

- 에피소드가 무한이면 MC와 TD는 같은 값에 수렴하는데, 에피소드가 만약 k개 밖에 없다면?



- Bootstrapping은 추측치(estimate)로 추측치를 업데이트, DP, TD가 해당
- Sampling은 하나의 샘플을 받아서 업데이트, MC, TD가 해당, DP는 가능한 액션들을 모두 해보고 저장하니까 샘플링을 안함
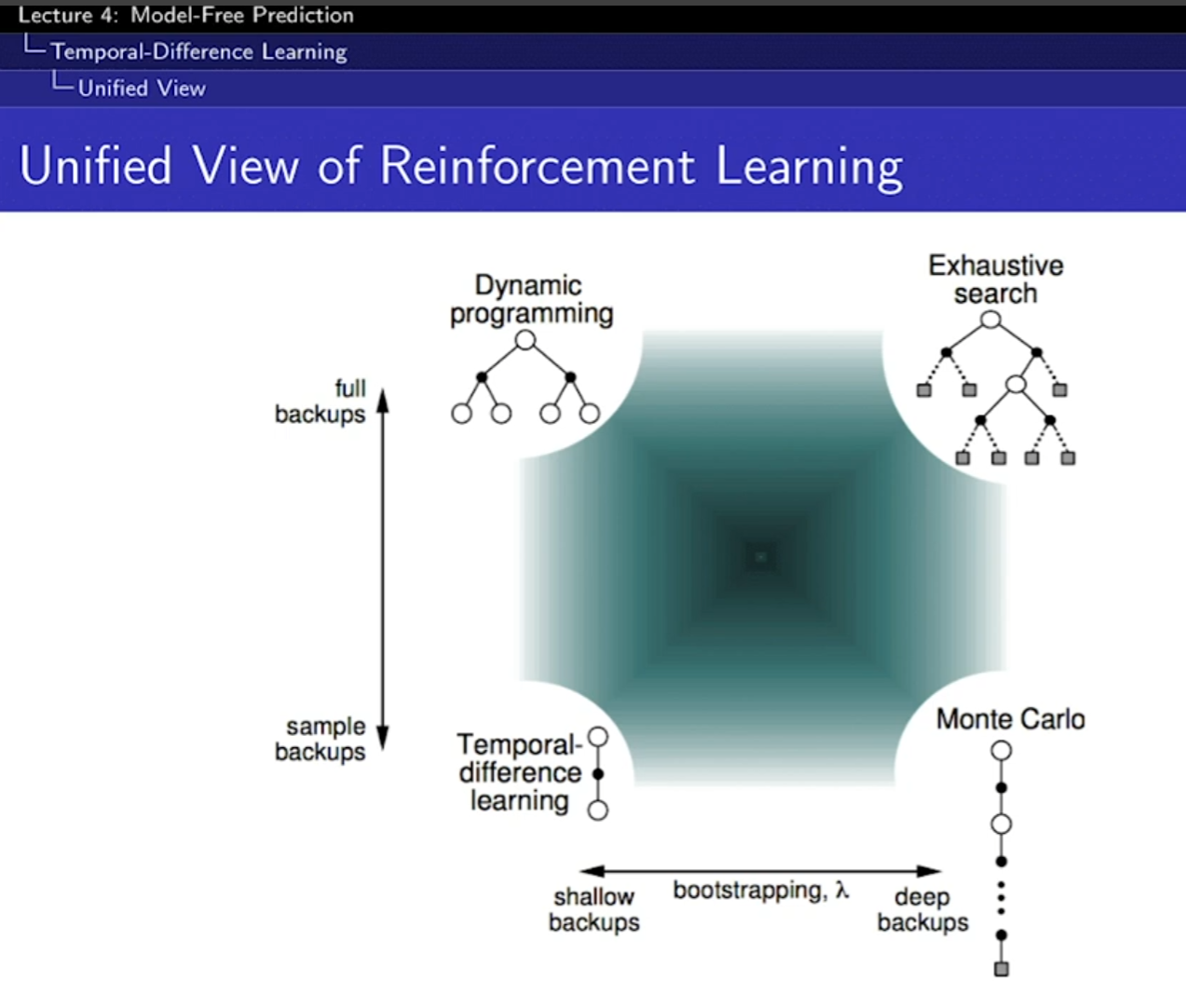
- Exhaustive search는 그냥 다 해보는 것. 다 해봐서 트리를 만듬

- TD는 몇 스텝을 가냐를 정해줄 수 있다. 스텝을 끝까지 가면 그게 MC 이다.

- 1스텝이 아니라, N스텝 학습도 가능하다. 2스텝, 4스텝을 한 것을 같이 평균내도 된다.

- TD(람다) 는 모든 스텝을 다 더해서 평균 낸 것, 논문에 자주 나온다.
- 무한 급수를 다 더하면 1이 나온다. 람다는 0~1 사이의
- Forward-view는 미래를 보는 것. backward-view는 과거를 보는 것이다.
- 사용 이유는 계산이 편하다.
- Forward-view는 단점으로 에피소드가 끝나야 학습이 가능하다. TD0의 장점이 사라진 것이다. 그래서 Backward-view를 사용


- Eligibility(적임) Traces
- 어떤 사건에 책임이 큰 것한테 더 큰 가중치를 주는 방법이다. 많이 발생한 순서에 따라 가중치를 주냐, 최근에 나온 것에 큰 가중치를 주냐 2가지 방법이 있다. 방문하면 1을 주고, 방문하지 않으면 0.9를 계속 곱해서 값을 낮춰준다. 따라서 최근 값, 반복되는 값이 모두 포함된다.
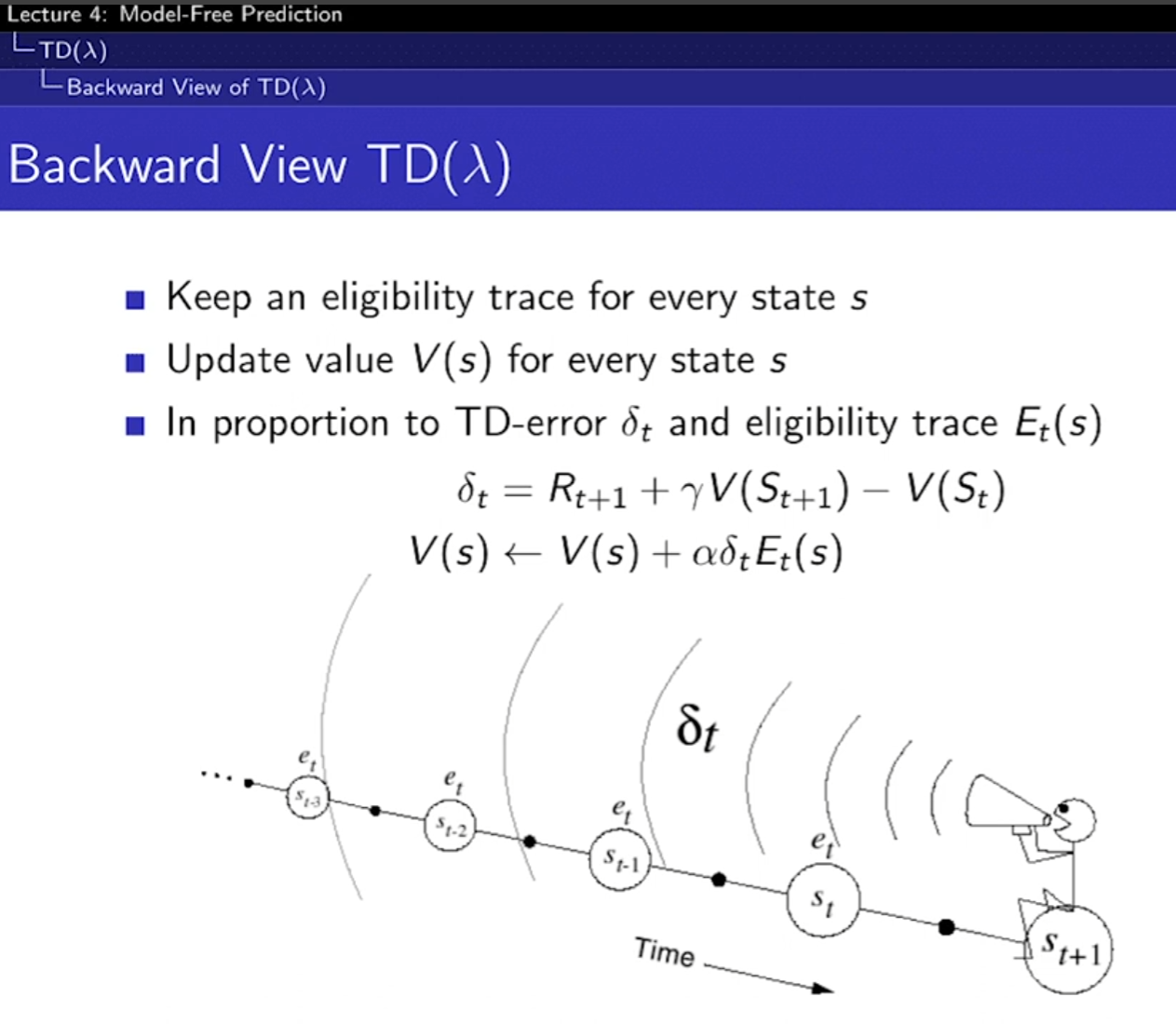
- 과거의 책임 소재(값)을 기록하고 가져오기 때문에 매 스텝마다 업데이트 할 수 있어 유용하다. 결국 수학적으로 TD(람다)의 값이 구해진다.

- TD(람다)는 오프라인으로 업데이트 하면 forward-view, backward-view와 같다.
- Online Updates: 온라인 업데이트는 각 시간 단계 후에 즉시 가치 함수를 업데이트합니다. 즉, 에이전트가 환경과 상호 작용하면서 새로운 정보를 받을 때마다 연속적으로 추정치를 업데이트합니다.
- Offline Updates: 오프라인 업데이트는 전체 에피소드가 완료된 후에만 가치 함수를 업데이트합니다. 이는 에피소드가 끝날 때까지 기다린 후, 수집된 데이터를 사용하여 한 번에 가치 함수를 업데이트하는 것을 의미합니다. 전체 상태와 보상의 시퀀스를 사용해야 하는 경우에 유용합니다.
'AI > 강화학습' 카테고리의 다른 글
| 1. [OpenAI] Spinning Up in Deep RL Introduction (1) | 2025.01.16 |
|---|---|
| Model Free Control (0) | 2024.06.25 |
| Planning by Dynamic Programming (0) | 2024.06.15 |
| Markov Decsion Processes(MDP) (0) | 2024.05.12 |
| 강화학습 소개(David Silver) (0) | 2024.05.11 |


